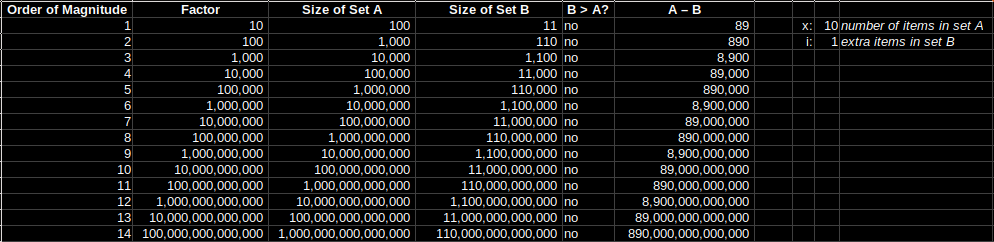
I wanted to get some intuition for what made a bigger difference: adding an extra item to a set, or having an extra order of magnitude of items in a set. So I created this spreadsheet and discovered that an extra order of magnitude smashes an extra item in the set.
In the spreadsheet the parameters are ‘x’, which is the size of the base set (called Set A), and ‘i’, which is the number of extra items to add into the second set (called Set B).
If you make x = 10 and i = 90 you break even, Set A and Set B grow at the same rate.
If you make x = 10 and i = 1 it’s no contest, Set A gets much bigger much faster.